Kľúčový rozdiel: V matematike sa na označenie rovnosti medzi dvomi výrazmi používa rovnica. Funkcia je na druhej strane oveľa zložitejšia ako rovnica. Funkcia sa používa na označenie vzťahu medzi množinou vstupov a množinou zodpovedajúcich výstupov.

Rovnica a funkcia sú dva zo základných základov algebry, predmetom matematiky. Obe môžu byť dosť zložité, avšak vo svojej základnej podobe môžu byť zmätené ako každý iný. Hlavným rozdielom medzi rovnicou a funkciou je skutočnosť, že rovnica sa zvyčajne zaoberá jedným vstupom, zatiaľ čo funkcia môže mať množstvo vstupov.

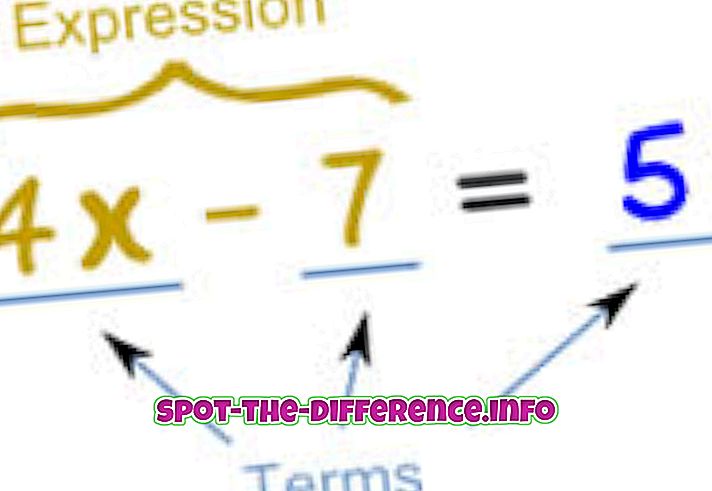
V matematike sa na označenie rovnosti medzi dvoma výrazmi používa rovnica. V podstate je rovnica napísaná ako výraz rovný inému výrazu. Napríklad: x + 2 = 5. To znamená, že čokoľvek je x, ak pridáte 2 k nemu, rovná sa 5. Preto môžeme vyriešiť rovnicu pre x, ktorá je 3, ako 3 + 2 = 5.

Rovnice môžu byť zložitejšie a môžu obsahovať viac ako jednu premennú, ako napríklad x, y, z, atď. V jednej rovnici. Napríklad: 3x + 2y - z = 4. Avšak každá abeceda bude zodpovedať jednému číslu. V tomto prípade x = 1, y = 2 a z = 3.

Z toho dôvodu,

3x + 2y - z = 4 sa stane

3 (1) + 2 (2) - 3 = 4, čo je

3 + 4 - 3 = 4 v podstate

4 = 4

Funkcia je na druhej strane oveľa zložitejšia ako rovnica. Funkcia sa používa na označenie vzťahu medzi množinou vstupov a množinou zodpovedajúcich výstupov. V podstate by vstup mal poskytnúť jeden výstup. Funkcia je vzťah medzi dvoma premennými. Napríklad: f (x) = x + 2. Podľa tejto funkcie, akokoľvek, vstup je, dá vám jeden výstup, ktorý bude vstup plus 2. Vyriešime túto funkciu:

vstup	funkcie	Výkon
X	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

A tak ďalej…

Funkcie majú rôzne aplikácie v oblasti matematiky, fyziky, informatiky atď. Môžu sa pohybovať od jednoduchých funkcií, ako sú uvedené vyššie, až po zložité vzorce alebo algoritmy. Funkciu možno považovať za stroj, ktorý poskytuje výstup pre vstup a výstup je nejakým spôsobom spojený so vstupom.

Funkcia má vždy tri časti: vstup, vzťah a výstup. Klasický spôsob zápisu funkcie je "f (x) = ...", kde x označuje vstup a f (x) označuje výstup.

Ako bolo uvedené vyššie, hlavným rozdielom medzi rovnicou a funkciou je, že rovnica má zvyčajne len jeden vstup, ktorý povedie k tomu, že výrazy budú rovnaké. Kým funkcia má rôzne vstupy, z ktorých každá prinesie výstup.